Граф пространства состояний при использовании алгоритма поиска в глубину

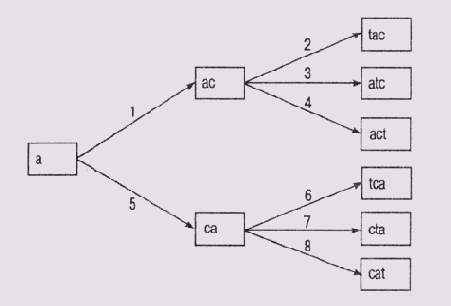
На обоих рисунках числа на дугах графа указывают номер шага, на котором формируется тот узел (состояние), для которого эта дуга является входящей. Конечно, этот номер еще зависит и от того, в каком порядке используются операторы из имеющегося множества. В представленном примере сначала применяется оператор, добавляющий очередную букву в конец последовательности, затем оператор, добавляющий букву на предпоследнюю позицию, и т.д., а последним применяется оператор, добавляющий букву на первое место. Но ведь можно использовать и обратный порядок применения операторов.

Оба алгоритма завершат работу (найдут конечное состояние) после формирования узла "act", а не "cat". Но алгоритму поиска в ширину придется для этого "посетить" пять узлов (сформировать и проанализировать пять состояний), а алгоритму поиска в глубину — четыре.

Отметим, что свойства этих алгоритмов существенно отличаются.

Алгоритм поиска в ширину отыскивает решение, путь к которому на графе — кратчайший, если таковое существует. Другими словами, он находит кратчайший путь между исходным состоянием и решением. Алгоритмы, обладающие таким свойством, называются разрешимыми (admissible).
Алгоритм поиска в глубину может быстрее найти решение, особенно, если при его выполнении используются эвристики для выбора очередной ветви. Но этот алгоритм может никогда не закончиться, если пространство состояний бесконечно.

Нетрудно заметить, что число узлов растет экспоненциально по мере увеличения числа уровней на графе. Это явление часто называют комбинаторным взрывом и оно представляет очень серьезную проблему при программировании таких задач, например при "грубом" переборе всех возможных вариантов позиций в игре в шахматы (см. врезку 2.1). Поскольку человеческий мозг слабее компьютера при решении задач, связанных с перебором вариантов, естественно предположить, что серьезный шахматист решает эту задачу каким-то другим способом. Скорее всего он использует свой опыт, воображение и аналитические способности, во-первых, для формирования общей стратегии игры, а во-вторых, для выбора наилучшего очередного хода. Вот такой-то способ решения мы и называем "интеллектуальным", в отличие от "грубого перебора".

В игровых программах также используется поиск в пространстве состояний, но стратегия поиска более избирательна, чем в случае прямого применения алгоритма generate-and-test. Кроме того, нужно принимать во внимание и то, что в игре, как правило, принимают участие две противоборствующие стороны. Были разработаны довольно неплохие программы для игры в шашки, нарды и шахматы. Созданные программы игры в шахматы нельзя отнести к классу систем, основанных на знаниях, а скорее к классу программ, обладающих способностью избирательно анализировать пространство состояний, что значительно повышает скорость и эффективность анализа. Методы и алгоритмы этого класса в данной книге рассматриваться не будут.

Другая задача, которая занимала умы исследователей в области искусственного интеллекта в середине 50-х годов, — доказательство теорем. Смысл задачи доказательства состоит в том, чтобы показать, как некоторое утверждение, которое требуется доказать (теорема), логически следует из декларированного множества других утверждений или аксиом (которые полагаются истинными или являются такими априори).