XML - статьи

Слабо-эквивалентные преобразования.


Определение 13 (Слабо-эквивалентные регулярные выражения) Два выражения r1 и r2 являются слабо-эквивалентными (r1? r2) , если для любой последовательности s=[s0..sn], такой что s|= r11 существует последовательность s'=[sk(0)..sk(n)] , где k есть подстановка на множестве {0,..,n} , такая что s'|= r2 и наоборот, для любой последовательности s=[s0..sn], такой что s|= r2 существует последовательность s'=[sk(0)..sk(n) , где k есть подстановка на множестве {0,..,n} , такая что s'|= r1 .

Утверждение 9 (Слабо-эквивалентные регулярные выражения) Следующие регулярные выражения являются слабо-эквивалентными:

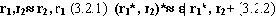
Докажем сначала первое утверждение. Пусть s=[s0..sn] |= r1,r2 . Тогда из определения 2 следует, что s [e0,…,ek, f0,..,fn], где [e0,…,ek] |=r1 и [f0,..,fn] |=r2 . Значит s' [ f0,..,fn ,e0,…,ek] |= r2, r1

Докажем второе утверждение. Пусть s|=(r1*, r2)* Рассмотрим два случая: s- пустая или непустая последовательность. Если s=[ ], то s|=? . Пусть s непустая последовательность символов. Тогда s можно представить в следующем виде

, где sji |= r1 , si |= r Тогда последовательность
=r1*,r2+ Что и требовалось доказать. В обратную сторону утверждение доказывается аналогично.

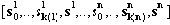
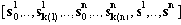
Определение 14 (Ослабленная интерпретация) Ослабленной интерпретацией I XML документа D в терминах структурной схемы S=(T,E,A,p,a,r) называется набор отображений I=(ф,?,?), удовлетворяющий всем свойствам интерпретации, кроме согласования содержания элемента. Условие согласования содержания элемента заменяется следующим:

    - (согласование содержания элемента) Пусть Ce = [e0,..,en] - есть упорядоченная последовательность элементов и текстовых узлов, вложенных в e. Тогда
    e
    ED: |(e k(0)),.., |(e k(n)) |= p(ф (e)), где k(i)- есть подстановка на множестве {0,..,n}

Определение 15 (Ослабленная Валидность) Документ D является ослабленно-валидным документом для структурной схемы S (слабо удовлетворяет схеме S), если существует ослабленная интерпретация I в терминах S (Обозначается D|? S).

Определение 16 (Слабая эквивалентность структурных схем) Схемы D и D' слабо эквивалентны, если множества слабо валидируемых XML документов каждой из этих схем совпадают.


Следующие утверждения являются очевидными и приводятся без доказательства.

Утверждение 10 ( Слабая эквивалентность эквивалентных регулярных выражений) Если регулярные выражения являются эквивалентными, то они являются слабо-эквивалентными.

Следствие 2 (Достаточное условие слабой эквивалентности) Если схема S и S' являются эквивалентными, то они являются слабо-эквивалентными.

Teoрема 4 (Критерий слабой эквивалентности схем, отличающихся только структурами) Пусть S=(T,E,A,p,a,r) и S'=( T,E,A,p',a,r) две структурные схемы, у которых множество валидируемых XML документов непустое, и отличающиеся только регулярными выражениями, задающими структурное вложение. Тогда схемы S и S' эквивалентны тогда и только тогда, когда
e
E p(e) ? p'(e)

Как будет показано в дальнейшем, в силу того, что при слабо-эквивалентных преобразованиях (замене регулярного выражения на слабо-эквивалентное) теряется только семантика порядка следования элементов, то их удобно использовать для трансляции из XML модели в модели, не использующие порядок в структурном описании.

Также, преобразование 3.2.2 ведет к "выравниванию" схемы (в английской литературе используется термин "flattening"), тем самым, приводя её к более простому виду - без вложенных операторов Клини (*).

Отдельно стоит заметить, что преобразование (r1, r2)* > r1*, r2* , часто встречающееся в алгоритмах трансляции XML модели в реляционную, не является слабо-эквивалентным.


Содержание раздела