Структурные ограничения XML

В этом разделе мы приводим формальное определение схем, состоящих из структурных ограничений, и формулируем термин "валидируемость". Также мы приводим определения эквивалентности схем и отношения порядка на схемах, которые будут использоваться в дальнейшем. Раздел начинается с определения регулярных выражений хорошо известных из литературы по грамматикам и языкам программирования.

Определение 1 (Регулярные выражения над множеством символов E) Множество регулярных выражений над множеством E (reg(E))определяется следующим образом:

Определение 2 (Порождаемые последовательности) Пусть r- регулярное выражение над множеством E. Тогда конечная (м.б. пустая) последовательность s=[e0,..,en] символов, где

, порождается выражением r (s|=r), тогда и только тогда, когда выполняется одно из следующих соотношений:

Множество всех порождаемых последовательностей регулярного выражения r над множеством Е называется регулярным множеством и обозначается так:

Пример 1

Пусть E={0,1}.
Множество последовательностей, порождаемых регулярным выражением (0|1)(0|1) состоит из множества последовательностей длины 2, содержащих элементы 0 и 1:

[0,0];[0,1];[1,0];[1,1].

Регулярное выражение (0|1)* порождает множество последовательностей произвольной длины, состоящих из 0 и 1, то есть полное множество всех последовательностей над множеством E.

Определение 3 (Эквивалентность регулярных выражений) Пусть r1,r2

reg(E) . Тогда

Определение 3' (Эквивалентность регулярных выражений)Пусть r1,r2

reg(E) . Тогда

Пример 2

Регулярные выражения r*,r и r+ эквивалентны, где r - произвольное регулярное выражение над множеством r. Покажем это. Пусть s|= r+ . Тогда по определению 2 s ? [s1,..,sn], где

i: si |=r. Тогда s1|=r и [s2,..,sn]|=r* и, значит, s|= r*,r . В обратную сторону утверждение доказывается аналогично.

Teoрема 1 (Замена выражений) Пусть

1 и 2 - есть идентичные регулярные выражения над множеством {E,r1} и {E,r2}, соответственно ,где r1 и r2- обозначения регулярных выражений над множеством E (f1 получается из f2 путем замены символа r2 на r1 и наоборот). Пусть 1 и 2 - это два регулярных выражения над множеством E, получаемые, соответственно, из 1 и 2, с помощью замены символов r1 и r2 на регулярные выражения над множеством E. Тогда r2 r1 ==> 1

Например, из этой теоремы следует, что выражение a|a+ a|(a*,a), так как a+ (a*,a)

Определение 4 (Структурные схемы XML документов) [12] Структурная схема XML документов есть совокупность (T,E,A,p,a,r), где:

• 
  
  T - множество, состоящее из всевозможных доменов.


Е - множество типов элементов; тип элемента состоит из имени и условного обозначения, являющегося уникальным идентификатором типа

A - множество типов атрибутов. Каждый тип включает в себя:

• 
  
  имя атрибута,


домен принимаемых значений
• 
  
  идентификатор обязательности (должен ли атрибут быть заполнен)


уникальный идентификатор типа атрибута

p есть функция из множества E в reg({E,T}) . p:E reg({id(E),T}), где id(E)- множество уникальных идентификаторов типа элемента

a есть функция из множества E в множество всех подмножеств множества A - pows(A). a: E pows(A), причем для любого типа элементов e типы атрибутов из множества a(e) должны обладать уникальным именем.

r E и называется типом корневого элемента. Для Множества E должно быть соблюдено следующее условие: e0 E, e ? r (e0,e1,..,en): i < n ei E и последовательность s=[a0,..,aj-1,ei,aj,..an] s { id(E),T} (p(ei+1)), en=r. Это условие означает "достижимость до любого элемента от корня"

Определение, данное выше, является достаточно универсальным способом спецификации структурных ограничений схем XML. Достаточно легко показать, что структурные ограничения, заданные выражениями на таких языках спецификации схем, как XML Schema, DTD, Relax NG отображаются в структурные схемы. В качестве примера, мы приведем пример отображения схемы, выраженной на языке DTD в структурную схему:

Пример 3



Данной схеме DTD соответствует структурная схема (T,E,A,p,a,r), где:

T {#PCDATA}

E {{Product, product}, {Name, name}, {Developer, developer},
{Summary, summary}

,{Description, description },{Para, para },{List, list}, {Item, item}, {Link, link}} (здесь и далее тип элемента
представляется как пара - {имя, Идентификатор})

A {(URL, CDATA, Required,url)}


p:

p(product)= (name, developer?, summary?, description?)



p(name)= p(Developer)=p(Summary)= #PCDATA

p(description)= (para | list)+

p(para)=p(Item) = (#PCDATA | link)*

p(list)= Item+

p(link)= ?

a:

a(link)={URL}

a(product)=a(name)=...=a(list) {}

r=product

Таким образом, можно установить, что при отображении в структурную схему каждому имени элемента в DTD соответствует уникальный тип элемента. Множество T состоит из типа #PCDATA (Термин PCDATA обозначает произвольный набор символов, интерпретируемый синтаксическим анализатором как текстовый узел). Каждому атрибуту соответствует свой тип атрибута, значения которого устанавливаются согласно свойствам типа атрибута в DTD. Наконец, отображение p задается исходя из регулярных выражений, определяющих структуру элемента DTD. Однако, стоит отметить, что ограничения целостности, которые могут присутствовать в DTD (атрибуты типа ID или IDREF) никоим образом не отображаются на структурную схему. Ограничения целостности мы обсудим в последнем разделе работы.

Заметим, что в зависимости от регулярного выражения, соответствующего элементам их типы можно классифицировать следующим образом:

- элементы пустого содержания : p(e)

{? },

- элементы, содержащие данные : p(e)

reg(T)/{? },

- элементы элементного содержания: p(e)

reg(id(E))/ {? },

- элементы смешанного содержания : p(e)

reg({id(E),T})/{ reg(E)

reg(T)}

В нашем примере, link -это элемент пустого содержания, name, developer, summary - элементы содержащие данные, product , description и list - элементного содержания, и наконец para и item - смешанного.

Стоит заметить, что структурные схемам вида (T,E,A,p,a,r) однозначно соответствуют регулярные грамматики деревьев [13], если положить следующее:

- множество F и id(Е) являются нетерминальными символами грамматики, где F - множество типов текстовых узлов, id(E) - множество уникальных идентификаторов типов элементов

- T и name(E) - терминалы грамматики, где name(E) - множество имен элементов

- Отображение p(e) заменяется правилом продукции одного из следующих двух видов:
x

a r, где x

id(E), a

name(E), r

reg({E,F}) или



x

a ? ,где x

F, a

T

В следующем разделе, мы опишем классы регулярных грамматик и их соответствие языкам спецификаций схем.

Следующие определения описывают понятие валидируемости XML документа. Здесь и далее, XML документ рассматривается в рамках модели XML , представленной в первой главе.

Определение 5 (Интерпретация) Интерпретация I XML документа D в терминах структурной схемы S=(T,E,A,p,a,r) - это набор отображений I=(ф ,? ,? ), где

• 
  
  ф - это отображение ED, -множества элементов документа, на множество E


? - это отображение AD, -множества атрибутов документа на множество A

? - это отображение TD, - множества текстовых узлов документа на множество T

Также должны выполняться следующие условия:

• 
  
  (согласование имен элементов)Пусть name - функция, ставящая в соответствие узлу документа его имя. Тогда
  
  e
  
  ED: name(e)= name (ф (e))


(согласование имен и значений атрибутов)Пусть value- функция, ставящая в соответствие узлу документа его значение. Тогда

a

AD: name(a)= name (? (a)) , value(a)

dom(? (a)), где dom(x) - это домен принимаемых значений типа атрибута

(согласование текстовых узлов)

t

TD: value(t)

? (t)

(согласование атрибутов с элементами)Пусть Ae={ai} i=[0,..,ne] - множество атрибутов элемента е. Тогда

e

ED:

i

[0,.., ne] ? (ai)

; a(ф(e))

(согласование обязательных атрибутов) ф-1(es) - множество элементов документа D, которые отображаются в тип элемента es. Также пусть R(es) - это подмножество a(es), в которое входят те и только те типы атрибутов, у которых проставлен идентификатор обязательности. Тогда

es

E

as

R(es)

e

ф-1(es)

a

Ae : ?(a)= as

(согласование корневого элемента) Для rD - корневого элемента документа D : ф( rD)=r

(согласование содержания элемента)Пусть Ce = [e0,..,en] - есть упорядоченная последовательность элементов и текстовых узлов, вложенных в e. Тогда

e

ED: I(e0),.., I(en) |= p(ф (e)), где I(ei) - это одно из двух отображений {ф ,? } (в зависимости от типа узла)

Определение 6 (Валидность) Документ D является валидным документом для структурной схемы S (удовлетворяет схеме S), если существует интерпретация I в терминах S (Обозначается D|=S).



Данное определение является ключевым для всего дальнейшего рассмотрения. Введем следующее обозначение: DB(S) - множество всех документов XML, удовлетворяющих данной схеме.

Утверждение 1 (Корректность валидности) Пусть D - схема, выраженная на языке спецификации DTD и S - соответствующая ей структурная схема. Тогда DB(D) DB(S). Если схема D не содержит ограничений целостности, тогда DB(D)=DB(S).

Для доказательства утверждения достаточно использовать свойства отображения схем DTD в структурные схемы (они очевидно следуют из примера 3).

Аналогичные утверждения можно сформулировать и доказать для других языков спецификации схем.

Заметим, что далеко не всегда существует единственная интерпретация одного и того же документа. Нижеследующий пример демонстрирует случай множественной интерпретации одного и того же документа.

Пример 4

На рис. 1 представлена структурная схема и документ XML



рис. 1 а) структурная схема б) документ

Документ XML содержит три элемента: A, B и C. Исходя из определения интерпретации, отображение I должно ставить в соответствие каждому элементу тип элемента из множества Е с таким же именем, как и у элемента. Поэтому в любой интерпретации элементу A соответствует тип a, элементу С тип с. А вот для элемента B существует два разных типа в которые он мог бы отображаться b1 и b Достаточно легко убедиться, что в обоих случаях будут выполняться условия интерпретации.

Определение 7 (Тривиальные схемы) Структурная схема называется тривиальной, если существует и притом единственный XML документ, валидный для данной схемы.

Утверждение 2 (Существование тривиальной схемы) Для любого XML документа существует тривиальная структурная схема, для которой данный документ валиден.

Для доказательства утверждения достаточно воспользоваться индукцией по глубине документа XML - максимальному расстоянию от корня дерева XML до листа. База индукции при n= В этом случае документ XML должен иметь следующий вид (представление в терминах модели XML [1]) - рис 2



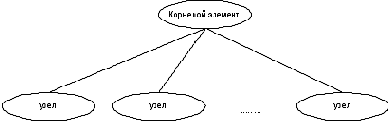
Рис 2 XML документ глубины 1



Как видно из рисунка, все узлы дерева помимо корня являются листами. Для формирования структурной схемы, необходимо выполнить следующие действия:

Множество E формируется следующим образом: для каждого узла типа "элемент", мы создаем отдельный тип элемента

Множество A формируется следующим образом: для каждого узла типа "атрибут", мы создаем отдельный тип атрибута. Доменный тип состоит из одного значения - значения данного узла в документе

Множество T формируется следующим образом: для каждого текстового узла в документе мы создаем отдельный домен, состоящий только из одного значения

Отображение a задается по следующим правилам: для любого типа элемента e - множество a(e) состоит из типов атрибутов, соответствующих атрибутам того элемента XML, который задавал e.

Отображение e задается по следующим правилам: для любого типа элемента e - p(e) - это выражение вида (e0,..,en) где ei это либо тип элемента, либо домен, задаваемый i-м дочерним узлом того элемента XML, который задавал e.

Тип элемента r (корневой тип) задается корневым элементом дерева XML.

Легко убедиться, что исходный документ удовлетворяет данной схеме. Также любой XML документ, удовлетворяющий данной схеме, совпадает с исходным документом. То есть схема является тривиальной. Индуктивный переход осуществляется следующим образом. Пусть утверждение доказано для документа, максимальная глубина которого равна n. Пусть у нас есть документ XML глубины n+1. В терминах XML модели, его можно представить в виде дерева глубины n+1. Рассмотрим множество поддеревьев, с корнями в дочерних узлах корневого документа исходного дерева. Их максимальная глубина не превышает n. По предположению индукции им ставится в соответствие тривиальные схемы. Общая схема формируется путем объединения множеств E,T,A каждой из этих тривиальных схем и продлением отображений a и p . Затем мы формируем еще один тип элемента r, соответствующий корню исходного XML документа, и продляем отображения a и p на него. Отображение a(r) возвращает множество атрибутов корневого элемента, а p(r)=(r0,..,rn), где ri - корневой тип элемента тривиальной схемы, порожденный i-м узлом.

Способ создания тривиальной схемы, использованный в утверждении 2, задает инъективное отображение множества документов XML на множество схем. Этот результат используется в работе [15] для реализации алгоритмов трансляции выражений алгебры управления структурными схемами в выражения языка запроса к данным XML. Легко показать, что все домены из множества T - доменных типов тривиальной схемы содержат в точности одно значение.

Лемма 1 (Достаточное условие тривиальности) Любая схема S=(T,E,A,p,a,r) такая, что для любого типа элементов e, регулярное выражение p(e) имеет вид r1,..,rnn, где ri есть символы базового алфавита, является тривиальной или пустой схемы.


Содержание раздела

---