Упрощающие преобразования.
Все преобразования, которые будут представлены ниже, ведут к потере определенной, достаточно большой части информации о структуре документа. Однако они достаточно часто используются на практике. Обусловлено это тем, что упрощение структурных ограничений приводит к существенному уменьшению сложности решения многих задач, встречающихся на практике.
Определение 17 (Упрощение регулярного выражения) Регулярное выражение r2 над E является упрощением р.в. r1 над E (r1 < r2) , если множество символов E, формирующих r2 , совпадает с множеством символов, формирующих r1, и выполняется следующее условие. Для любой последовательности s=[s0..sn] такой, что s|= r1 существует последовательность s'=[sk(0)..sk(n)] , где k есть подстановка на множестве [0,n] и s'|= r
Утверждение 3. Для регулярных выражений r1 и r2
- r1 < r2, r2 < r1 < = > r1 ? r2,
r1

Для доказательства первого предложения в прямую сторону (r1 < r2 , r2 < r1==> r1 ? r2) достаточно воспользоваться определением упрощения. Чтобы доказать утверждение в обратную сторону, необходимо воспользоваться критерием допустимости символов из множества E (теорема 2). Вторая часть утверждения вытекает и первой и из утверждения 10
Из этого утверждения непосредственно вытекает, что слабо-эквивалентные и эквивалентные преобразования являются упрощающими.
Утверждение 4. (Упрощающие преобразования) Следующие преобразования регулярных выражений являются упрощающими:
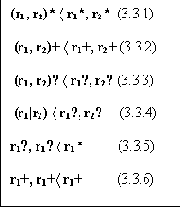
Доказательство этого утверждения напрямую следует из определения порождаемых последовательностей. Заметим, что мы перечислили не все упрощающие преобразования.
Пример 5
Дано следующее описание элемента : < !ELEMENT a ((b|c|e|)?,(e?|(f?,(b,b)*))*)>

Как видно из примера исходная схема приобретает весьма простой вид. Следует учесть, что информация об относительном порядке элементов утеряна, но при этом семантика множественности сохранена (например, элемент с может быть максимум один у элемента а).
Определение 18 (Упрощение схемы) Схемы D' является упрощением схемы D, если множество валидируемых документов первой схемы принадлежит множеству слабо-валидируемых элементов второй.
Критерий и достаточное условие того, что схема S является упрощением схемы S', формулируются и доказываются таким же образом, как и для слабо-эквивалентных схем.
В следующем разделе, мы определим нормальные формы схем XML документов и докажем теоремы существования нормальных форм произвольных структурных схем.
